RGB 图像做直方图均衡（看三个通道与整个图像做直方图是否一样）

惊喜地发现这就是我在实验一研究过的问题了。

现在知道了，RGB 空间每个通道即有颜色信息又有亮度。因此，如果单独针对每个通道做直方图均衡，必然导致均衡过的图三个通道的权重改变，与整个图做直方图均衡结果不同。

	I=imread('MizunoAi.jpg');
	subplot(2,3,1);imshow(I);title('原始图像');subplot(2,3,4);imhist(I);
	c=histeq(I);
	subplot(2,3,2);imshow(c);title('直方均衡化·调库');subplot(2,3,5);imhist(c);
	c=cat(3,histogram(I(:,:,1)),histogram(I(:,:,2)),histogram(I(:,:,3)));
	subplot(2,3,3);imshow(c);title('直方均衡化');subplot(2,3,6);imhist(c);
function J=histogram(I)
	J=I;
	[n,m]=size(I);
	a=zeros(1,256);
	b=zeros(1,256);
	for i=1:n
		for j=1:m
			a(1,I(i,j)+1)=a(1,I(i,j)+1)+1;
		end
	end
	sum=0;
	for i=1:256
		sum=sum+a(1,i);
		b(1,i)=255*sum/(m*n);
	end
	for i=1:n
		for j=1:m
			d=J(i,j)+1;
			J(i,j)=b(1,d);
		end
	end
end

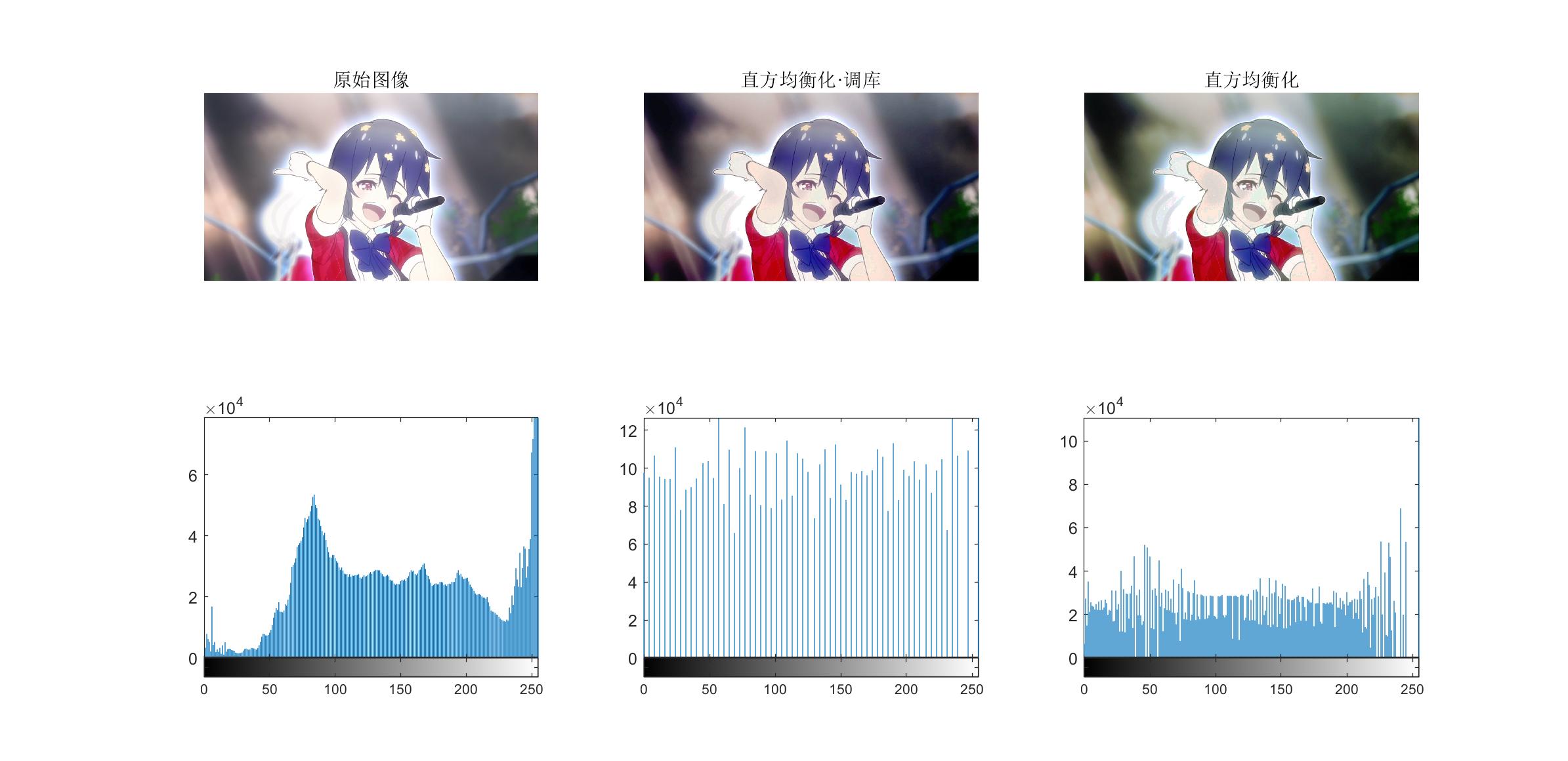
可以看到，三个通道分别做直方图均衡化和整个图像做直方图均衡化的结果相比偏绿了。

利用带阻滤波器消除周期性噪声

原理分析

高斯带阻滤波器的公式为$H(i,j)=1-e^{-\frac{1}{2}[\frac{D(u,v)W}{D^2(u,v)-D_0^2}]^2}$

源代码

I=imread('3.jpg');
[m,n]=size(I);

H=zeros(m,n);%构造高斯带阻滤波器
d0=100
w=3
for i=1:m
    for j=1:n
        H(i,j)=1-exp(-0.5*(((i-m/2)^2+(j-n/2)^2-d0^2)/(sqrt(i.^2+j.^2)*w))^2);
    end
end

F=fftshift(fft2(I));
subplot(2,2,1)
imshow(log(1+abs(F)),[])
title('原图频谱图（经过对数处理）')

J=F.*H;%频率域滤波
subplot(2,2,2)
imshow(log(1+abs(J)),[])
title('带阻滤波器处理后的频谱图（经过对数处理）')

J=ifft2(ifftshift(J));
J=abs(J);
J=J/max(J(:));%归一化

subplot(2,2,3)
imshow(I)
title('原图')

subplot(2,2,4)
imshow(J)
title('带阻滤波器处理后的图')

运行结果

仔细可以看到原图频谱图上有四个亮点（对数处理的还不是很明显）。这里经过调参，发现他们在半径 100 的圆上。因此据此设置带阻滤波器的半径d0=100和宽度w=3.

可以看到，带阻滤波器对这样的周期性噪声处理效果是非常好的。